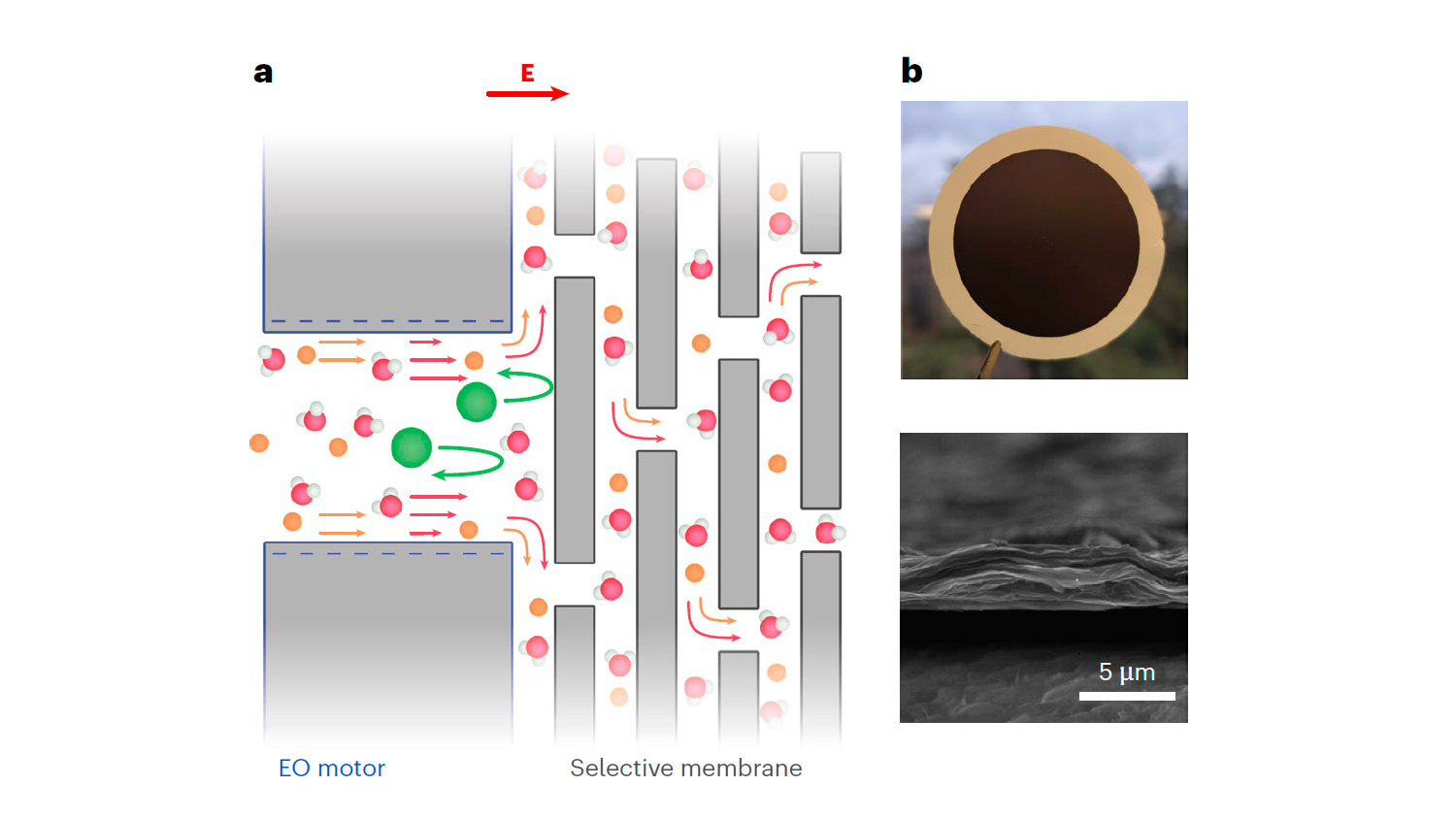
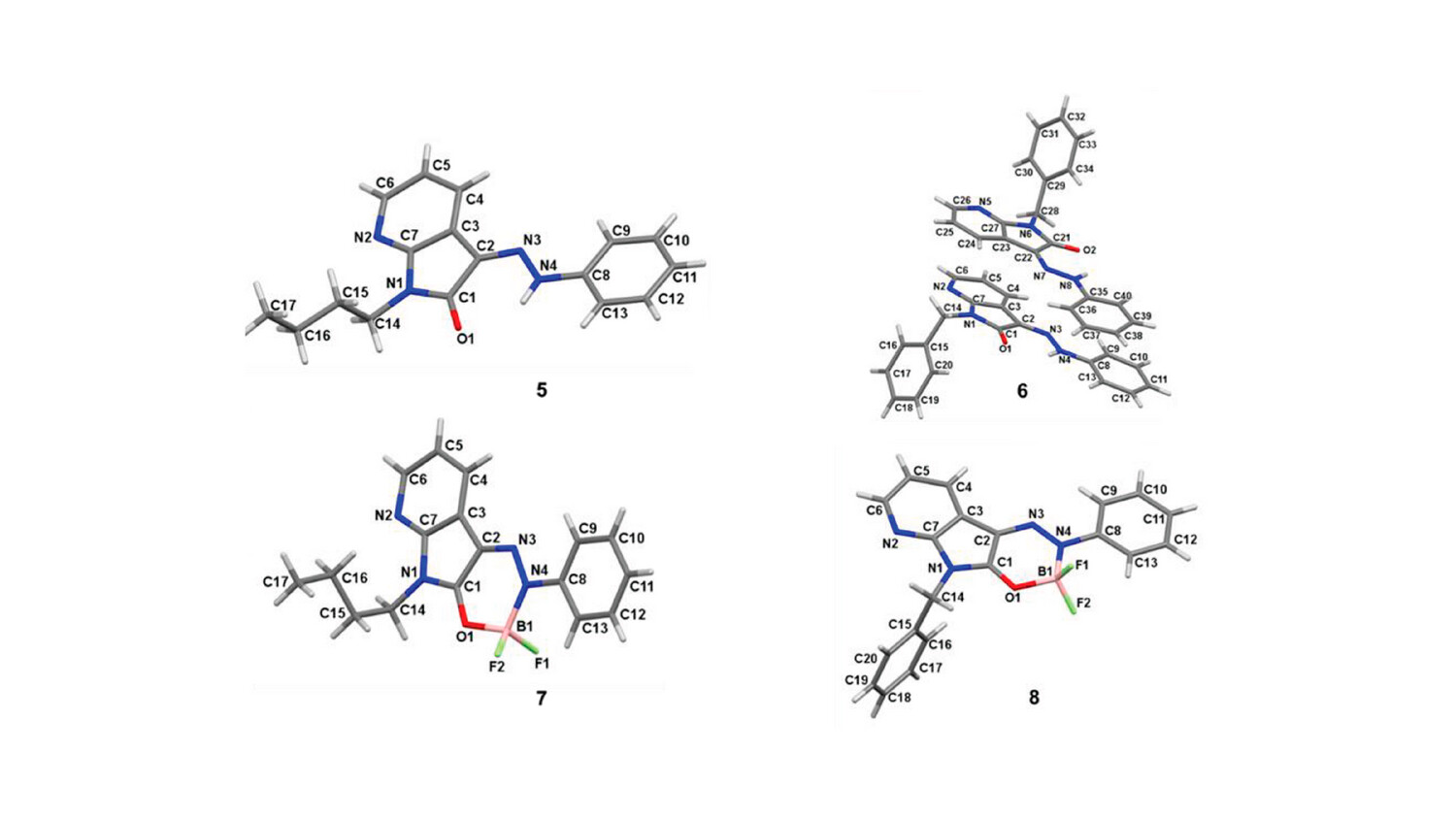
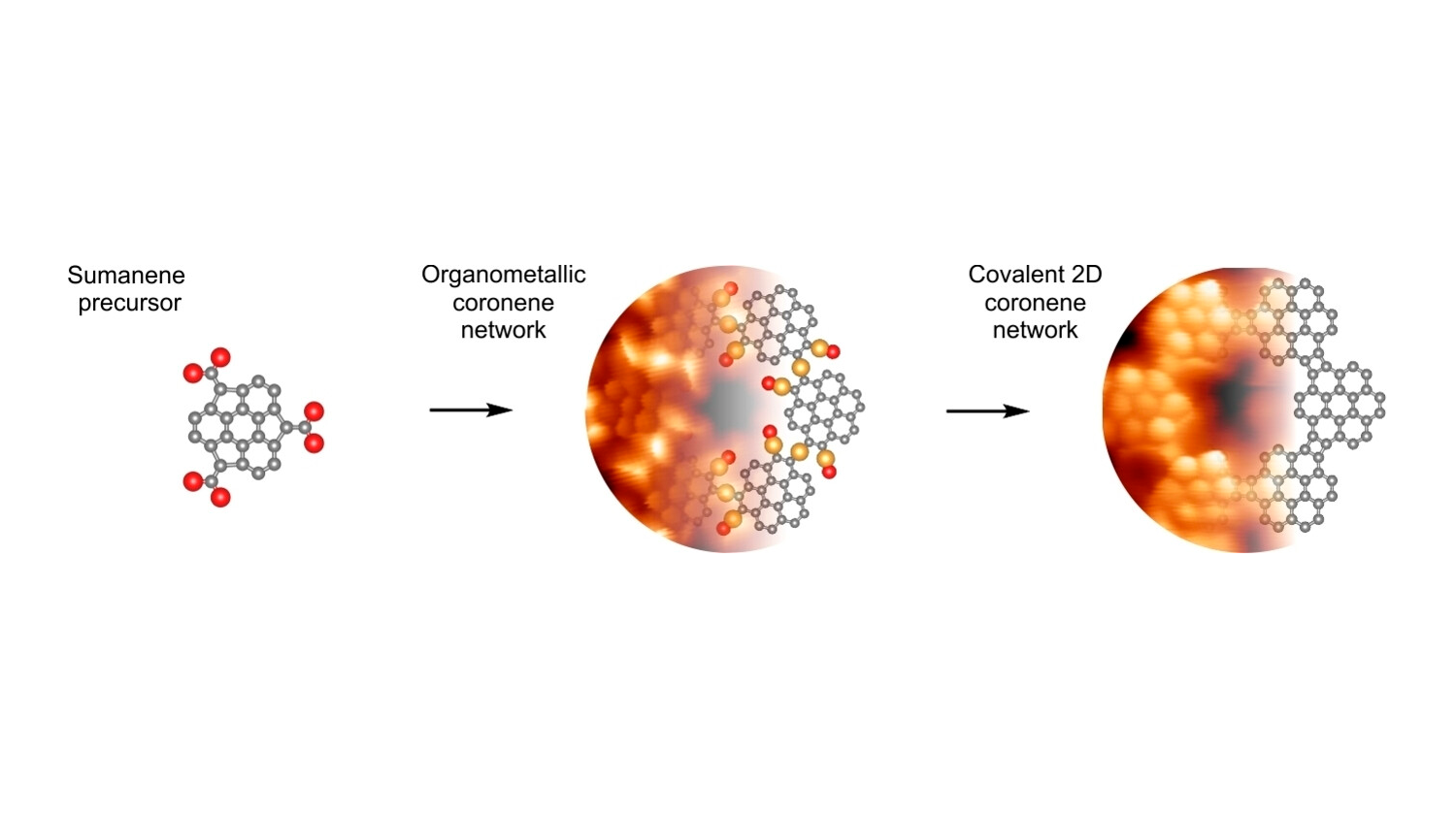
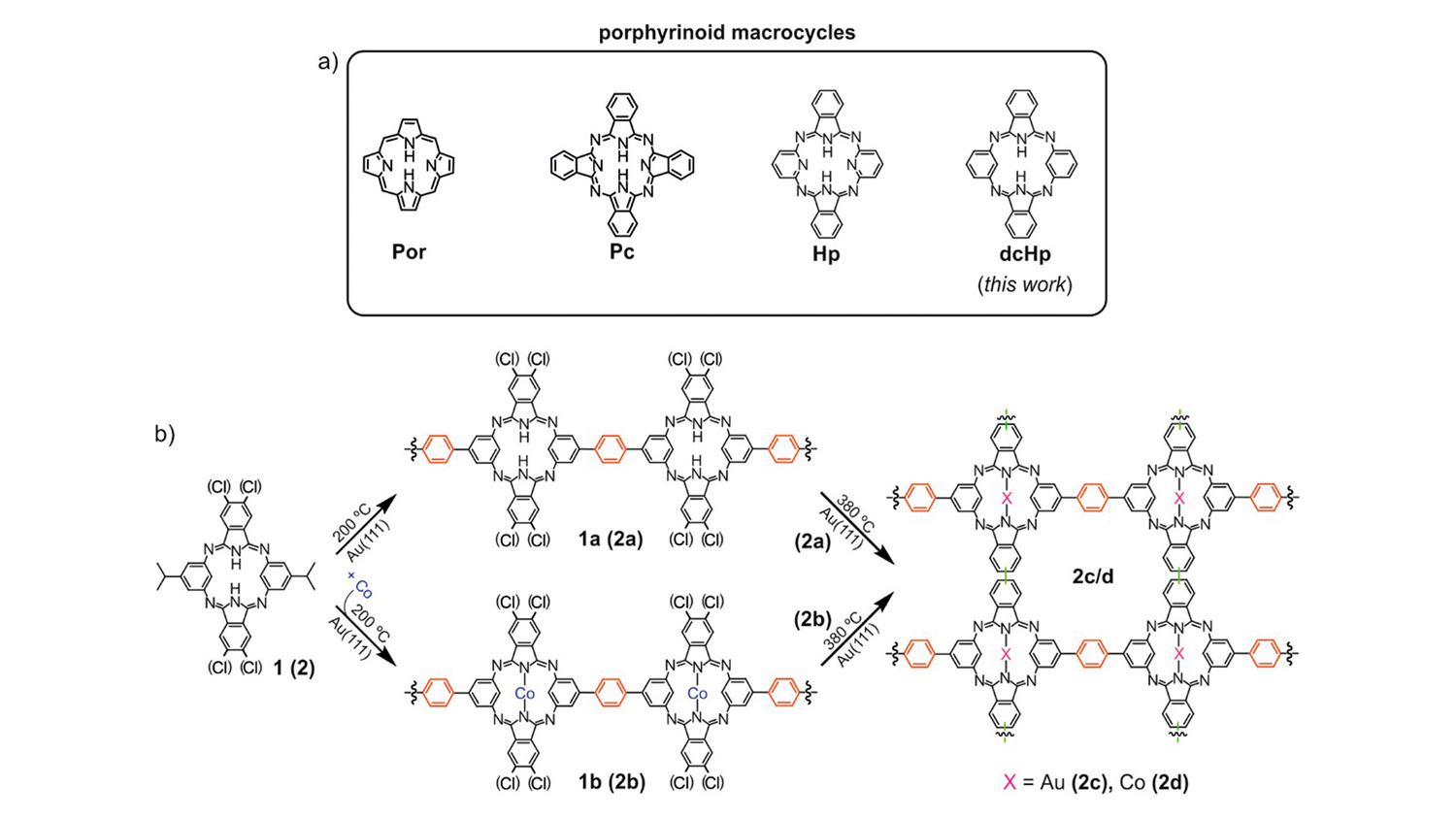
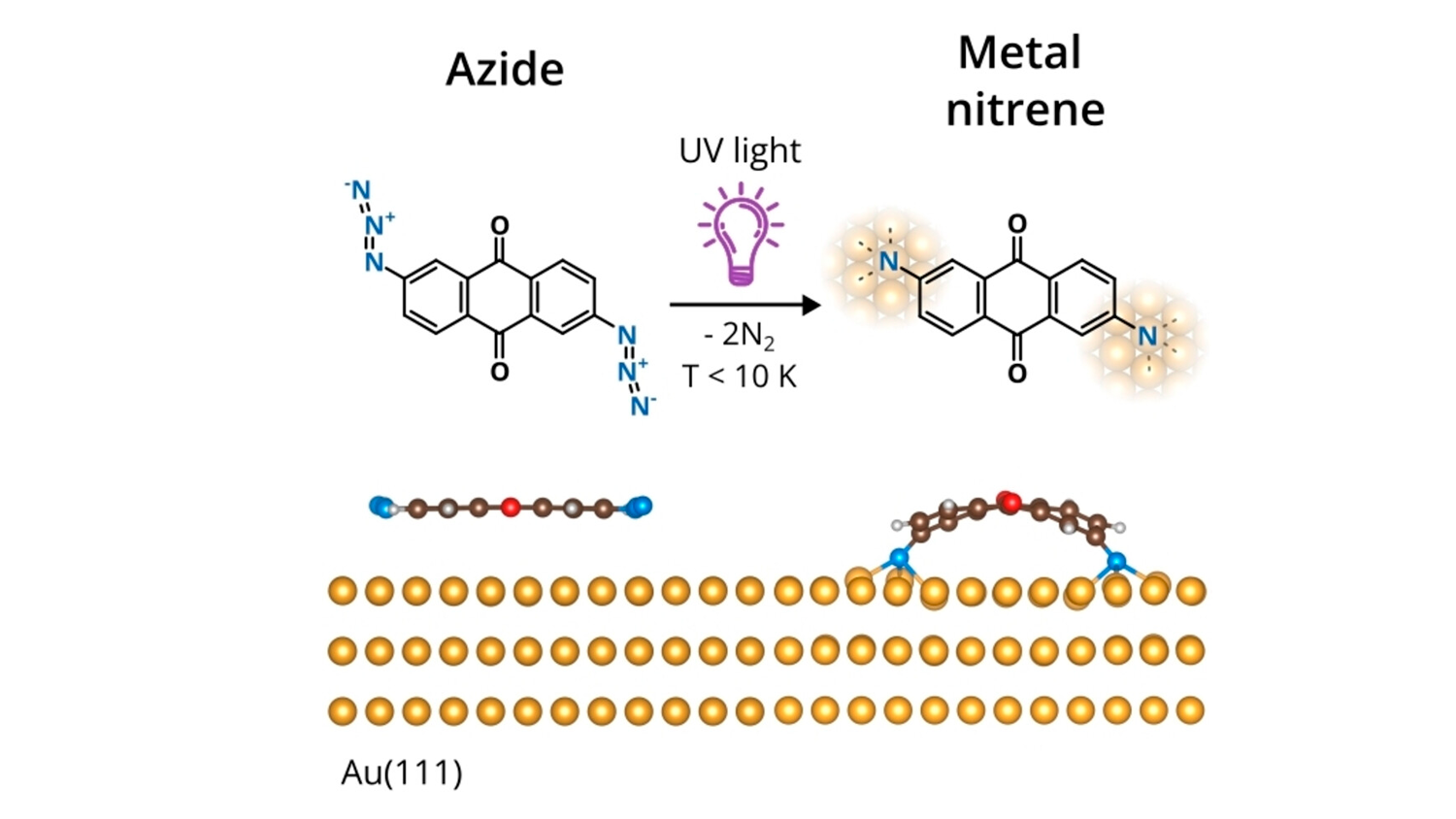
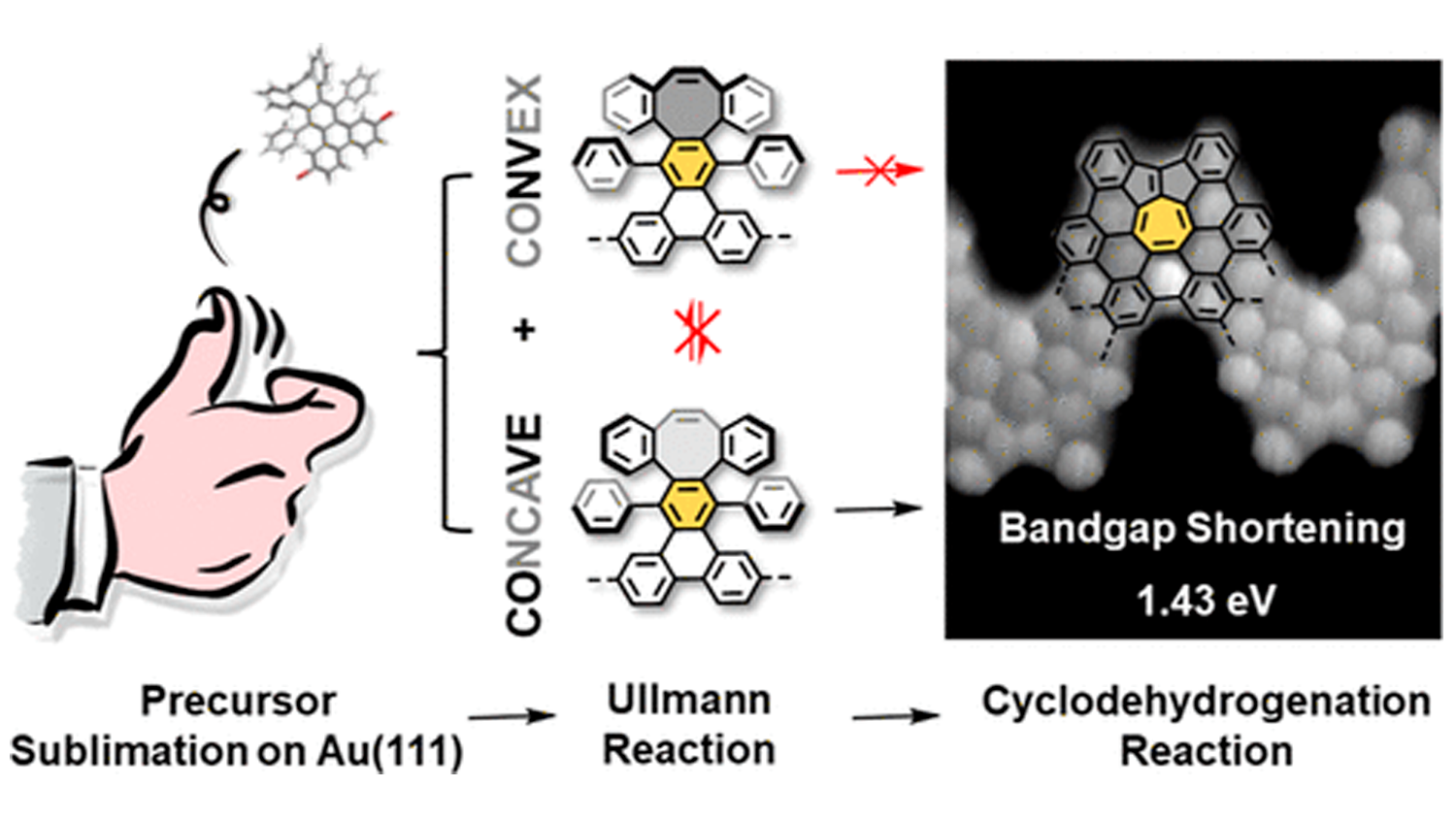
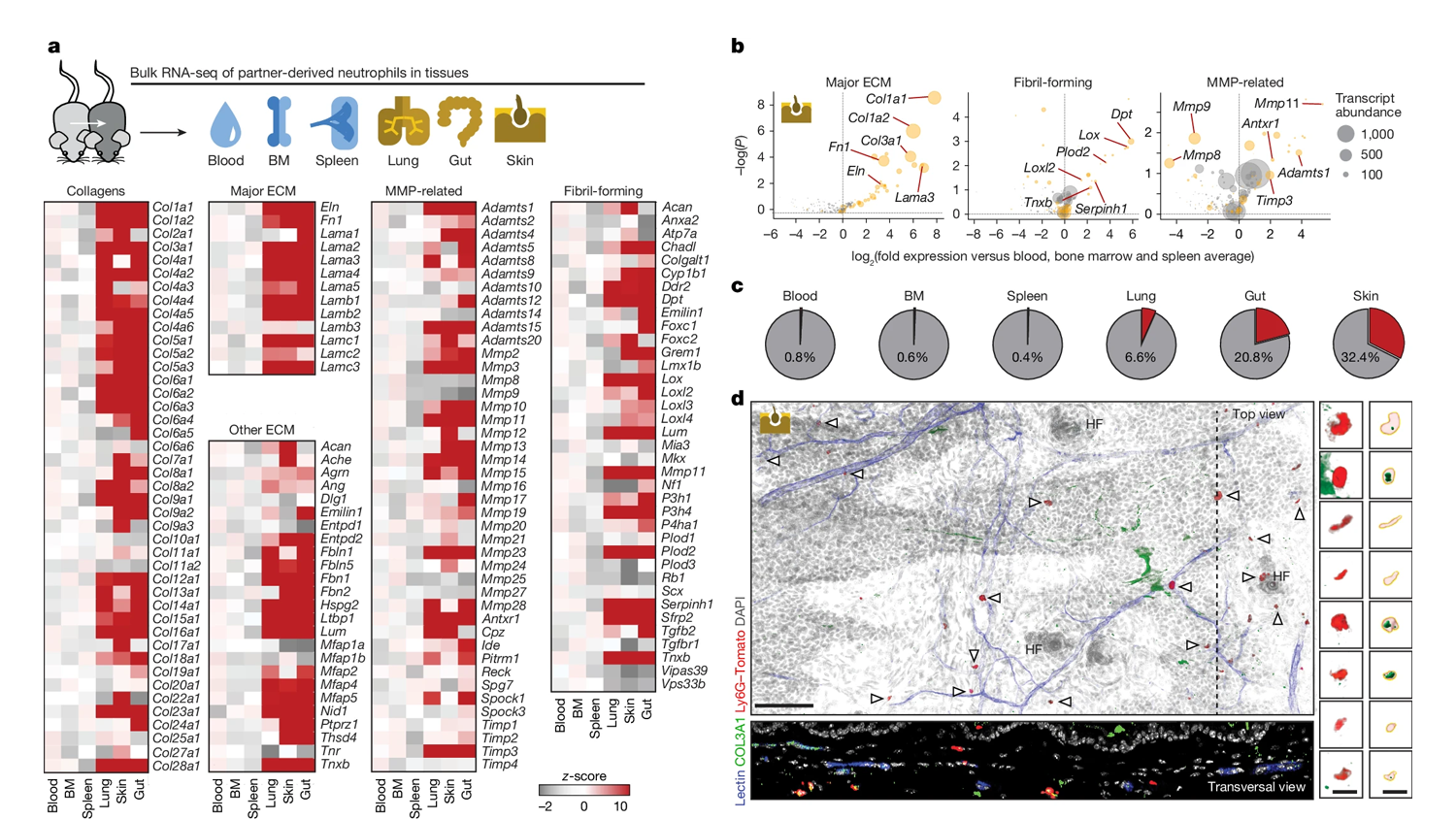
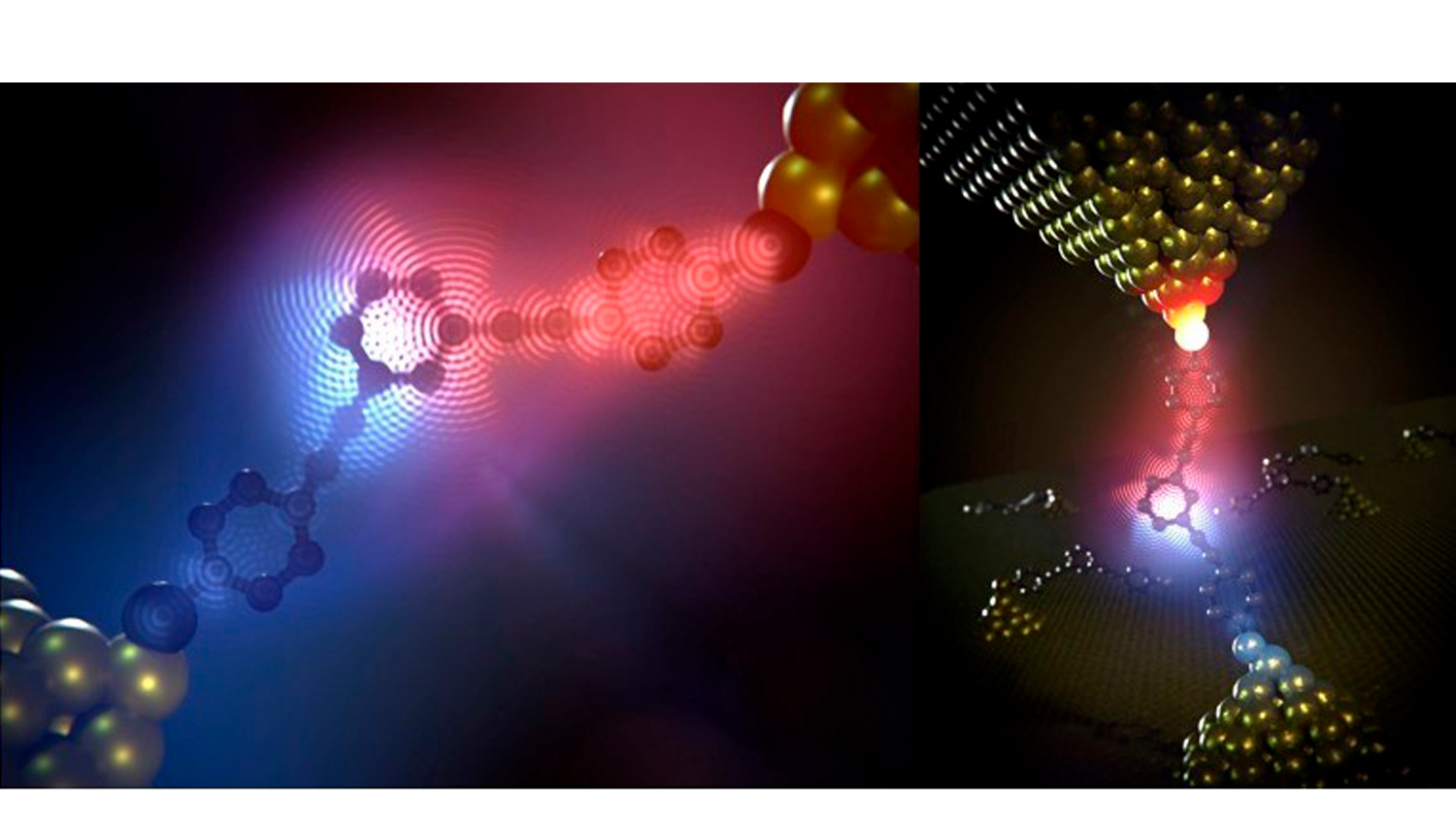
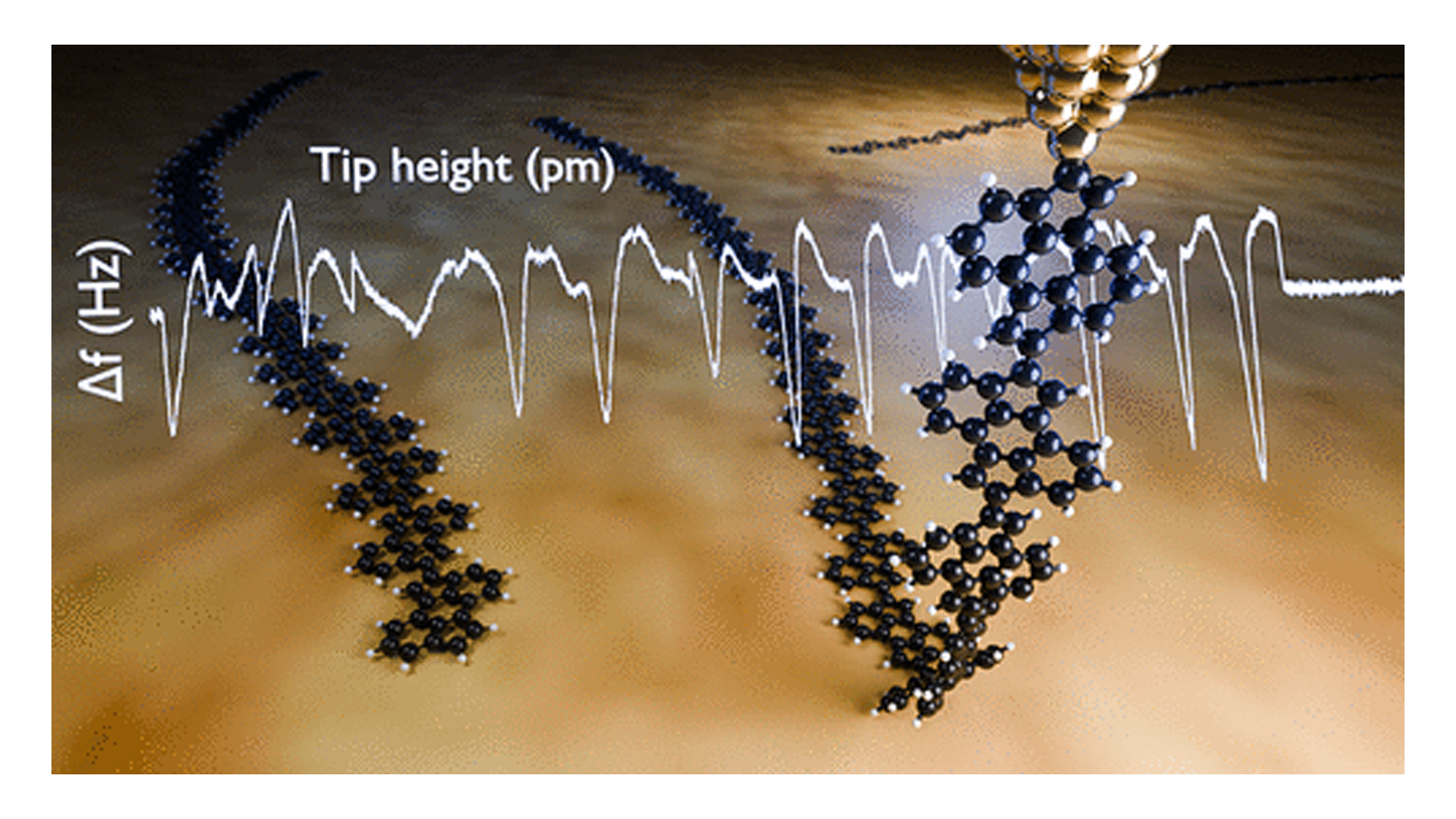
Está dotado con más de 5,5 millones de euros. "Es un reconocimiento al esfuerzo de todo un centro, tanto de personal investigador de todos los niveles como de administración, de servicios científico-técnicos y personal de apoyo", celebra José Ángel Martín-Gago, director del ICMM-CSIC y profesor de investigación del CSIC.
10000
Noticias
Welcome
5000
ICMM
Sor Juana Ines de la Cruz, 3
Cantoblanco, 28049
Madrid, España
Teléfono: (+34) 91 334 90 00
Email: @email
Oficina de Comunicación/Prensa: @email


Contacto | Accesibilidad | Aviso legal | Política de Cookies | Protección de datos